Construction of the bisector of the angle

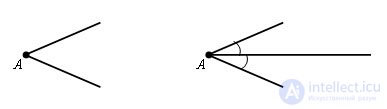
Build a bisector of this angle.

Decision



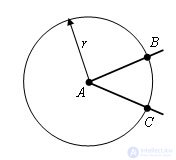
From the vertex A of this angle, as from the center, we describe a circle of arbitrary radius r. Let B and C be the points of its intersection with the sides of the angle.



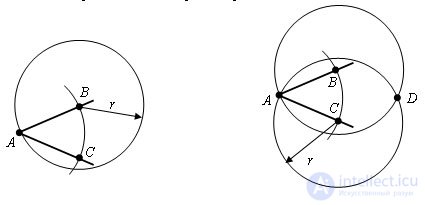
From points B and C we draw circles with the same radius r. Let point D be their intersection point different from A.



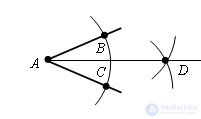
We will hold the beam AD.



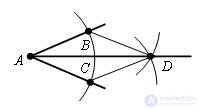
Conduct the segments BD and CD. Δ ABD = Δ ACD, on the third sign of equality of triangles. Hence, ∠ BAD = ∠ CAD and therefore AD is the bisector of the angle BAC.