Given the segments a, b, c. Build the segment x = bc / a.
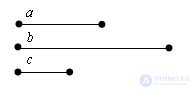
Decision.
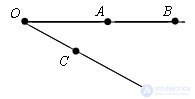
We construct any non-maximized angle with vertex O. On one side of the angle, we will plot the segments OA = a, OB = b, and on the other side, the segment OC = c.
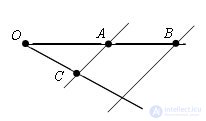
Connect points A and C, and through point B we draw a straight line parallel to (AC).
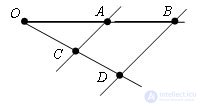
Let D be the intersection point of this line with the ray OC. The segment OD is the desired one.
Evidence.
According to the theorem on proportional segments: OA / OB = OC / OD
Therefore, OD = OB * OC / OA = b * c / a is the desired segment x.
The constructed segment is called the fourth proportional, because it is the fourth term of the proportion a: b = c: x.




Comments
To leave a comment
Planometry
Terms: Planometry