The cosine of the acute angle of a right triangle is the ratio of the adjacent leg to the hypotenuse.
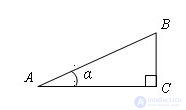
The cosine of the angle α is denoted by: cos α.
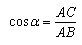 Theorem
Theorem The cosine of the angle depends only on the degree measure of the angle and does not depend on the location and size of the triangle.
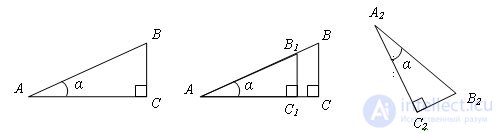 Evidence.
Evidence. Let Δ ABC and Δ A2B2C2 be given - right triangles. ∠ A = ∠ A2 = ∠ α. It is required to prove that
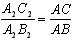
Construct Δ AB1C1 equal to A2B2C2. Straight lines B1C1 and BC are perpendicular to AC and therefore parallel to each other. Then, by the proportional segments theorem

A pop building A2C2 = AC1 and A2B2 = AB1, then
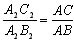
The theorem is proved.

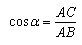

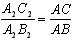

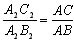
Comments
To leave a comment
Planometry
Terms: Planometry