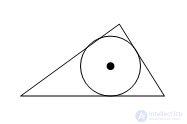
A circle is said to be inscribed in a triangle if it touches through all its sides.
Theorem.
The center of a circle inscribed in a triangle is the intersection point of its bisectors.
Evidence.
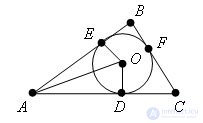
Let ABC be given, O be the center of the circle inscribed in it, D, E, and F be the points of tangency of the circle with the sides. Δ AEO = Δ AOD on the hypotenuse and the leg (EO = OD - as the radius, AO - total). It follows from the equality of triangles that ∠ OAD = ∠ OAE. This means that the AO bisector of the angle EAD. Similarly, it is proved that the point O lies on the other two bisectrices of the triangle. The theorem is proved. |
|
Comments
To leave a comment
Planometry
Terms: Planometry