Center line of a triangle

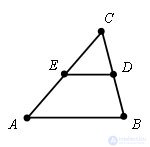
The middle line of a triangle is a segment connecting the midpoints of its two sides.



Theorem.

The middle line of the triangle connecting the midpoints of these two sides is parallel to and equal to a third side.



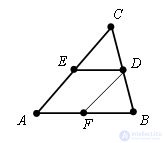
Evidence.

Let Δ ABC and its mean line ED be given.
Let us draw a straight line parallel to the side AB through point D. According to the Thales theorem, it intersects the segment AC in its middle, i.e. matches with DE. This means that the middle line is parallel to AB.
We now draw the middle line DF. It is parallel to the AC side. The quadrilateral AEDF is a parallelogram. By the property of the parallelogram ED = AF, and since AF = FB by the theorem of Thales, then ED =? AB. The theorem is proved.