Two figures are called
similar if they are translated into each other by a similarity transformation.
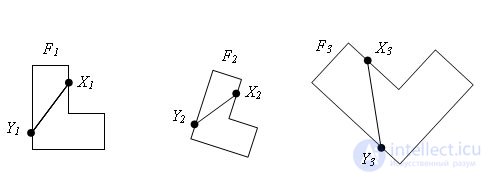 Theorem
Theorem If the figure F1 is similar to the figure F2, and the figure F2 is similar to the figure F3, then the figures F1 and F3 are similar.
Evidence. Let points X1 and Y1 be two arbitrary points of the figure F1. When converting the similarity, the figure F1 goes into the figure F2, and the points X1 and Y1 go to X2 and Y2 so that X2Y2 = k1 * X1Y1
Accordingly, the similarity transformation translates the figure F2 into F3 and X3Y3 = k2 * X2Y2.
Therefore, X3Y3 = k2 * X2Y2 = k2 * k1 * X1Y1.
As it can be seen, the transformation of the figure F1 to F3, resulting from the successive execution of two similarity transformations, is a similarity. So the figures F1 and F3 are similar. The theorem is proved.

Comments
To leave a comment
Planometry
Terms: Planometry