Central symmetry of the parallelepiped

Theorem

The diagonal of the parallelepiped intersect at one point and the intersection point is divided in half.



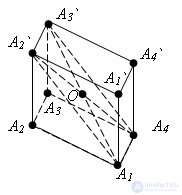
Evidence

Consider any two diagonal parallelepiped, for example A1A3 `and A4A2`. Since the quadrangles A1A2A3A4 and A2A2`A3`A3 are parallelograms with the common side A2A3, their sides A1A4 and A2`A3` are parallel to each other, therefore, lie in the same plane. This plane intersects the planes of the opposite faces of the parallelepiped along parallel straight lines A1A2` and A4A3`. Therefore, the quadrilateral A4A1A2`A3` is a parallelogram. The diagonal of the parallelepiped A1A3` and A2A4` are the diagonals of this parallelogram. Therefore, they intersect and the intersection point O is divided in half.
Similarly, it is proved that the diagonals A1A3` and A2A4`, as well as the diagonals A1A3` and A3A1` intersect and the intersection point is divided in half. The theorem is proved.

See also

• Ball symmetry
• Central symmetry of the parallelepiped
• The symmetry property about a point
• Symmetry relatively straight
• Symmetry about point
• Polyhedra