
Divide the segment in half.
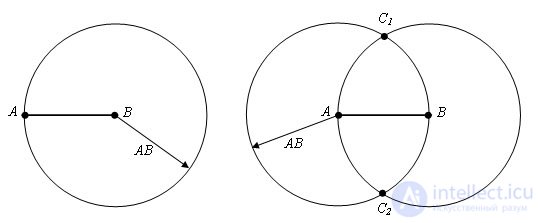
Let AB be a given segment. We describe a circle with radius AB with center at points A and B. Let these circles intersect at points C1 and C2.
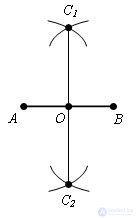
Points C1 and C2 lie in different half-planes from the straight line AB. Draw through the points C1 and C2 a straight line. Let it intersect the line AB at some point O. The point O is the midpoint of the segment AB.
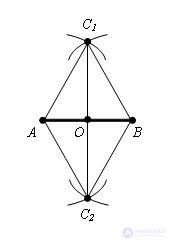
Evidence. Δ C1AC2 = Δ C1BC2 on the third sign of equality of triangles (AC1 = BC1, AC2 = BC2, by construction and C1C2 is common). Therefore, ∠ AC1C2 = ∠ BC1C2. This implies Δ AC1O = Δ BC1O on the second sign of equality of triangles (∠ AC1C2 = ∠ BC1C2, AC1 = BC1 by construction, OC1 is common). Therefore, AO = OB and O is the midpoint of the segment AB.




Comments
To leave a comment
Planometry
Terms: Planometry