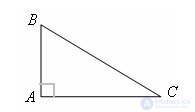
A triangle is said to be rectangular if it has a right angle. The side of a right triangle opposite to the right angle is called the hypotenuse, the other two sides are the legs. AC and AB - legs, BC - hypotenuse.
Theorem. If the hypotenuse and the leg of one right triangle are respectively equal to the hypotenuse and the leg of another right triangle, then such triangles are equal.
 Evidence.
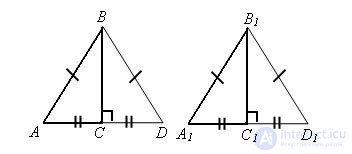
Evidence. Let ABC and A1B1C1 be triangles. Construct a triangle DBC equal to triangle ABC, and a triangle D1B1C1 equal to triangle A1B1C1.
Δ ABD = Δ A1B1D1 on the third sign of equality of triangles (AB = A1B1, BD = B1D1, AD = A1D1) from this it follows that ∠ BAC = B1A1C1.
Δ ABC = Δ A1B1C1 on the first sign of equality of triangles (AB = A1B1, AC = A1C1, Δ ABC = Δ A1B1C1). The theorem is proved.


Comments
To leave a comment
Planometry
Terms: Planometry