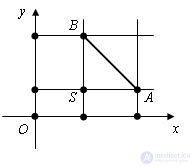
Given two points A (x1; y1) and B (x2; y2). Find the distance between points A and B.
Let us drop perpendiculars from points A and B to the abscissa axis and to the ordinate axis. As can be seen from the figure, a pair of perpendiculars intersect at point S. The distance between points B and S is | y1-y2 |, and the distance between points S and A is | x1-x2 |. We get the triangle SBA. According to the Pythagorean theorem
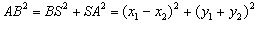
|
|
Comments
To leave a comment
Planometry
Terms: Planometry