Cartesian coordinates on the plane

We have two lines x and y that intersect at point O. These lines are called axes. The x axis is called the x-axis, and the y axis is the ordinate axis. The point of intersection of the axes is called the origin. Each axis splits the plane into two half-planes, one of them is positive, the other is negative.
We denote the plane Oxy (O is the intersection point of the x axis with the y axis).



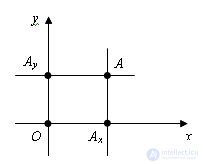
Any point on the plane, say the point A, you can associate a pair of numbers, this pair of numbers is called the coordinates of the point. They are defined as:
1) draw a straight line through point A parallel to the ordinate axis. This straight line will intersect the x-axis x at some point Ax. The number x, the absolute value of which is equal to the distance from point O to point Ax, is called the abscissa of point A.
2) draw a straight line through point A, parallel to the abscissa axis. This straight line will intersect the x axis at some point Ax. The number y, the absolute value of which is equal to the distance from point O to point Ay, is called the ordinate of point A.
If Ax belongs to the positive semiaxis, then this is a positive number, if negative is a negative number.
If Ay belongs to the positive semiaxis, then this is a positive number, if negative is a negative number.
If point A lies on the y-axis, then x = 0.
If point A lies on the x-axis, then y = 0.

The coordinates of point A are written like this: A (x; y).



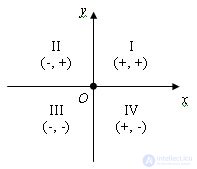
The plane is divided by coordinate axes into four parts - quarters: I, II, III and IV. Within one quarter, the signs of both coordinates are stored and have the meanings as in the figure.
The coordinates x and y entered on the plane are called Cartesian coordinates.