Lecture
Definition Any line on the plane can be given by a first order equation.
Ah + Wu + C = 0,
and the constants A, B are not equal to zero simultaneously. This first order equation is called the general equation of a line. Depending on the values of the constants A, B and C, the following special cases are possible:
• C = 0, A ≠ 0, B ≠ 0 - the straight line passes through the origin
• A = 0, B ≠ 0, C ≠ 0 {By + C = 0} - the straight line is parallel to the Ox axis
• B = 0, A ≠ 0, C ≠ 0 {Ax + C = 0} - the straight line is parallel to the axis Oy
• B = C = 0, A ≠ 0 - the straight line coincides with the axis Oy
• A = C = 0, B ≠ 0 - the straight line coincides with the axis Ox
The equation of a line can be represented in a different form depending on any given initial conditions.
Definition In a Cartesian rectangular coordinate system, a vector with components (A, B) is perpendicular to the straight line given by the equation Ax + Vu + C = 0.
An example . Find the equation of a line passing through point A (1, 2) perpendicular to the vector 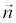 (3, -1).
(3, -1).
The decision . When A = 3 and B = -1, we make the equation of a straight line: 3x - y + C = 0. To find the coefficient C, we substitute the coordinates of the given point A into the resulting expression. We get: 3 - 2 + C = 0, therefore, C = -1 . Total: equation sought: 3x - y - 1 = 0.
Let two points M 1 (x 1, y 1, z 1) and M2 (x 2, y 2, z 2) be given in space, then the equation of a line passing through these points:
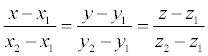
If any of the denominators is zero, the corresponding numerator should be equated to zero. In the plane, the equation of a straight line written above simplifies:
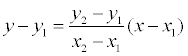
if x 1 ≠ x2 and x = x 1, if x 1 = x2.
Fraction 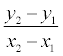 = k is called the slope of the line.
= k is called the slope of the line.
An example . Find the equation of a line passing through the points A (1, 2) and B (3, 4).
Decision. Applying the above formula, we get:
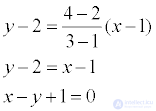
If the general equation of the line Ax + Wu + C = 0 is reduced to the form:
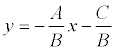
and mark 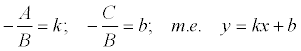 , then the resulting equation is called a straight line equation with a slope k .
, then the resulting equation is called a straight line equation with a slope k .
By analogy with the point considering the equation of a straight line through the normal vector, you can enter the specification of a straight line through a point and the directing vector of a straight line.
Definition Every nonzero vector 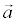 (α1, α2), whose components satisfy the condition A α1 + B α2 = 0 is called the direct vector of the vector
(α1, α2), whose components satisfy the condition A α1 + B α2 = 0 is called the direct vector of the vector
Ah + Wu + C = 0.
Example. Find the equation of a line with a guiding vector 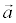 (1, -1) and passing through point A (1, 2).
(1, -1) and passing through point A (1, 2).
Decision. We will look for the equation of the desired line in the form: Ax + By + C = 0. In accordance with the definition, the coefficients must satisfy the conditions:
1 * A + (-1) * B = 0, i.e. A = B.
Then the equation of the line has the form: Ax + Ay + C = 0, or x + y + C / A = 0. for x = 1, y = 2, we get C / A = -3, i.e. equation sought:
x + y - 3 = 0
If in the general equation of the line Ax + Vu + C = 0 C ≠ 0, then, dividing by –C, we get: 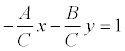 or
or
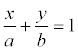 where
where
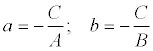
The geometrical meaning of the coefficients is that the coefficient a is the coordinate of the point of intersection of the straight line with the axis Ox, and b is the coordinate of the point of intersection of the line with the axis Oy.
Example. Given the general equation of the line x - y + 1 = 0. Find the equation of this line in the segments.
C = 1, 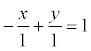 , a = -1, b = 1.
, a = -1, b = 1.
If both sides of the equation Ax + Wu + C = 0 multiply by the number 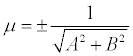 , which is called the normalizing factor , we get
, which is called the normalizing factor , we get
xcosφ + ysinφ - p = 0 -
normal equation of a line. The sign ± of the normalizing factor should be chosen so that μ * С <0. p is the length of the perpendicular dropped from the origin to a straight line, and φ is the angle formed by this perpendicular with the positive direction of the axis Ox.
An example . Given the general equation of the line 12x - 5y - 65 = 0. It is required to write various types of equations of this line.
the equation of this line in the segments: 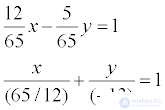
equation of this line with the slope: (divide by 5)
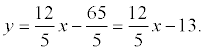
normal straight equation:
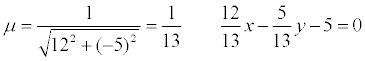 ; cos φ = 12/13; sin φ = -5/13; p = 5.
; cos φ = 12/13; sin φ = -5/13; p = 5.
It should be noted that not every straight line can be represented by an equation in segments, for example, straight lines parallel to the axes or passing through the origin.
An example . The straight line cuts equal positive segments on the coordinate axes. Make an equation of a straight line, if the area of the triangle formed by these segments is equal to 8 cm 2.
Decision. The equation of a line is: 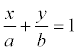 , ab / 2 = 8; ab = 16; a = 4, a = -4. a = -4 <0 does not match the condition of the problem. Total:
, ab / 2 = 8; ab = 16; a = 4, a = -4. a = -4 <0 does not match the condition of the problem. Total: 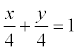 or x + y - 4 = 0.
or x + y - 4 = 0.
An example . Make an equation of a line passing through point A (-2, -3) and the origin.
The decision . The equation of a line is: 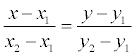 where x 1 = y 1 = 0; x2 = -2; y2 = -3.
where x 1 = y 1 = 0; x2 = -2; y2 = -3. 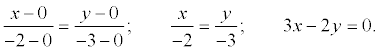
Definition If two straight lines y = k1 x + b1, y = k 2x + b2 are given, then the acute angle between these straight lines will be defined as
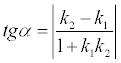 .
.
Two straight lines are parallel if k1 = k2. Two straight lines are perpendicular if k1 = -1 / k2.
Theorem. The lines Ax + Vu + C = 0 and A 1 x + B1 y + C1 = 0 are parallel when the coefficients A1 = λA, B1 = λB are proportional. If also C1 = λC, then the lines coincide. The coordinates of the intersection point of two lines are found as a solution to the system of equations of these lines.
Definition The straight line passing through the point M1 (x1, y1) and perpendicular to the straight line y = kx + b is represented by the equation:
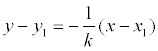
Theorem. If the point M is set (x0, y0), then the distance to the straight line Ax + Wu + C = 0 is defined as
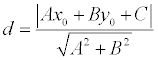 .
.
Evidence. Let the point M 1 (x 1, y 1) be the base of the perpendicular dropped from the point M to the given line. Then the distance between points M and M1:
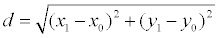 (one)
(one)
The coordinates x1 and y1 can be found as a solution to the system of equations:
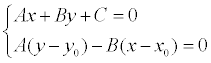
The second equation of the system is the equation of a straight line passing through a given point M 0 perpendicular to a given straight line. If we convert the first equation of the system to the form:
A (x - x 0) + B (y - y0) + Ax0 + By0 + C = 0,
then, deciding, we get:
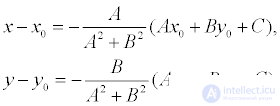
Substituting these expressions into equation (1), we find:
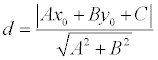
The theorem is proved.
An example . Determine the angle between the straight lines: y = -3 x + 7; y = 2 x + 1.
k 1 = -3; k 2 = 2; tgφ = 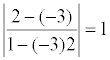 ; φ = π / 4.
; φ = π / 4.
An example . Show that the lines 3x - 5y + 7 = 0 and 10x + 6y - 3 = 0 are perpendicular.
The decision . We find: k 1 = 3/5, k2 = -5/3, k 1 * k 2 = -1, therefore, the lines are perpendicular.
An example . The vertices of the triangle A (0; 1), B (6; 5), C (12; -1) are given. Find the equation of height drawn from vertex C.
The decision . Find the equation of the side AB: 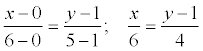 ; 4 x = 6 y - 6;
; 4 x = 6 y - 6;
2 x - 3 y + 3 = 0; 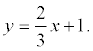
The sought height equation has the form: Ax + By + C = 0 or y = kx + b. k = 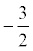 . Then y =
. Then y = 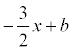 . Because when the height passes through point C, then its coordinates satisfy this equation:
. Because when the height passes through point C, then its coordinates satisfy this equation: 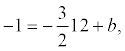 where b = 17. Total:.
where b = 17. Total:. 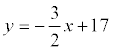
Answer: 3 x + 2 y - 34 = 0.
Comments
To leave a comment
Planometry
Terms: Planometry