Perpendicular straight lines

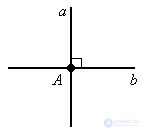
Two straight lines are called perpendicular if they intersect at a right angle.
Line a intersects line b at a right angle at point A. You can hang using the perpendicular icon: a ⊥ b. It reads like this: the line a is perpendicular to the line b.
It should be noted that the adjacent angle and the vertical angle with a right angle are also right.

Theorem

Through each point of a straight line it is possible to draw a straight line perpendicular to it, and only one.



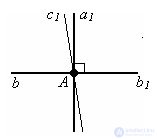
Evidence.

Let b be a given straight line, and point A belongs to this straight line. Take a ray b1 on a straight line b with a starting point in A. Let the angle (a1b1) equal to 90 ° from the beam b1. By definition, a straight line containing a1 is perpendicular to b.
Suppose there is another straight line perpendicular to b and passing through point A. Take on this straight line c1, coming from point A and lying in the same half-plane as ray a1. Then ∠ (a1b1) = (c1b1) = 90 º. But according to axiom 8, only one angle equal to 90 º can be laid in this half-plane. Consequently, it is impossible to draw another straight line perpendicular to the straight line b through the point A into the given half-plane. The theorem is proved.





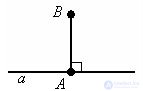
Perpendicular to this line is called a line segment, perpendicular to this line, having one of their ends at the intersection point. This end of the segment is called the base of the perpendicular. AB is perpendicular to the line a. Point A is the base of the perpendicular.