Theorem If two sides of one triangle are proportional to two sides of another triangle and the angles formed by these sides are equal, then the triangles are similar.
 Evidence.
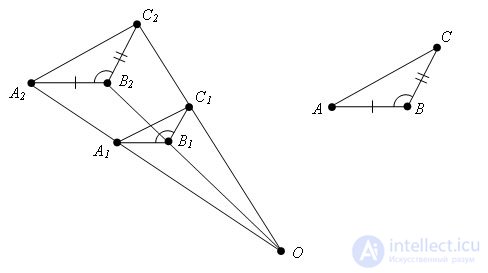
Evidence. Let the triangles ABC and A1B1C1 ∠ CBA = ∠ C1B1A1, AB = k * A1B1, BC = k * B1C1. Let us prove that Δ ABC is similar to Δ A1B1C1.
Subject Δ A1B1C1 homothety with coefficient k. Get some Δ A2B2C2.
Δ A2B2C2 = Δ ABC on the first sign of equality of triangles (∠ A2B2C2 = ∠ A1B1C1 = ∠ ABC since the similarity transformation preserves angles, A2B2 = k * A1B1 = AB, B2С2 = k * B1С1 = BС, by condition).
Triangles A1B1C1 and A2B2C2 are homothetic, hence similar. Δ A2B2C2 = Δ ABC, therefore are similar too, which means that triangles A1B1C1 and ABC are similar. The theorem is proved.

Comments
To leave a comment
Planometry
Terms: Planometry