Lecture
Two half-lines are called equally directed or co-directed if they are combined by a parallel translation. That is, there is a parallel transfer that translates one half direct to another.
If the half-lines a and b are the same direction and the half-lines b and c are the same direction, then the half-lines a and c are also the same direction (Fig. 1) .
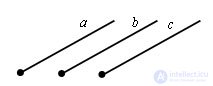
Indeed, let the parallel transfer defined by the formulas
x '= x + m , y' = y + n, (*)
translates the semi-direct a into the semi-direct b , and the parallel transfer defined by the formulas
x "= x '+ m 1 , y" = y' + n 1 (**)
translates semi-direct b to semi-direct c .
Consider the parallel transfer defined by the formulas
x "= x + m + m 1 , y" = y + n + n 1 . (***)
We assert that this parallel transfer takes the half-line a to the half-line with . Let's prove it.
Let (x; y) be an arbitrary point of the half-line a . According to formulas (*), the point (x + m; y + n) belongs to the half-line b .
Since the point (x + m; y + n) belongs to the half-line b , according to formulas (**) the point (x + m + m 1 ; y + n + n 1 ) belongs to the half-line c .
Thus, the parallel transfer defined by the formulas (***) translates the half-line a into the half-line with. This means that the half-lines a and c are equally directed, which is what was required to prove.
Two half-lines are called
oppositely directed, if each of them is equally directed with a half-line, complementary to the other (Fig. 2).

Figure 2 - oppositely directed semi-straight lines.
Example Task .
Straight AB and CD are parallel. Points A and D lie on one side of the secant aircraft. Prove that the rays BA and CD are equally directed. 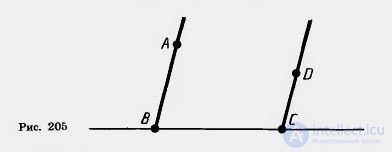
The decision . Let's put the CD beam to parallel transfer, at which point C goes to point B (fig. 205).
In this case, the direct CD will be aligned with the direct VA.
Point D, shifting in a straight line parallel to the SV, remains in the same half-plane with respect to the straight sun.
Therefore, the CD beam will align with the AA beam, which means that these rays are equally directed.
Comments
To leave a comment
Planometry
Terms: Planometry