Theorem
The area of the parallelogram is equal to the product of its side by the height drawn to this side S = a • h.
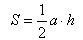
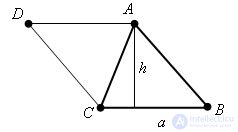 Evidence
Evidence
Let ABC be a given triangle. We add it to the parallelogram ABCD.
The area of the parallelogram is equal to the sum of the areas of triangles ABC and CDA. Since these triangles are equal, the area of the parallelogram is equal to twice the area of the triangle ABC. The height of the parallelogram corresponding to side CB is equal to the height of the triangle drawn to side CB. This implies the statement of the theorem, and
The theorem is proved.
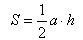

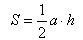
Comments
To leave a comment
Planometry
Terms: Planometry