Two vectors are called equal if they are combined by a parallel translation.
Those. there is a parallel translation, in which the beginning and end of one vector is combined with the beginning and end of another vector, respectively.
Theorem
If the vectors are equally directed and equal in absolute value, then they are equal.
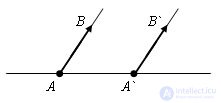
Evidence.
Let AB and CD be equally directed vectors equal in absolute value. The parallel transfer, which translates the point A` to the point A, combines the beam A`B` with the beam AB, because they are co-directed. The segments AB and A`B` are equal, therefore the point B coincides with the point B`. This means that a parallel transfer translates the vector A`B` into the vector AB. So the vectors are equal. The theorem is proved. |
|
Comments
To leave a comment
Planometry
Terms: Planometry