A four gon is a figure that consists of four points (the vertices of a quadrilateral) and four segments connecting these points in series (the sides of a quadrilateral). Wherein:
1. no three data points lie on the same line;
2. the segments connecting these points must not intersect.
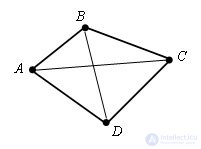
Points A, B, C, D are the vertices of the four squares.
The segments AB, BC, CD, DA are the sides of the quadrilateral.
The vertices of the four squares are called adjacent vertices if they are the ends of one of its sides. For example, vertices A and B are adjacent.
Vertices that are not adjacent are called opposite vertices. For example, vertices A and C are opposite. The segments that connect the opposite vertices of a quadrilateral are called diagonals. AC and BD are the diagonals of the quadrilateral.
The sides of a quadrilateral emanating from one vertex are called adjacent (adjacent) sides. For example, AB and BC are neighboring sides. Parties that do not have common vertices are called opposite sides. For example, AB and CD are opposite sides.
A quad is indicated by its vertices, for example ABCD. In the designation of a quadrilateral, adjacent vertices must be adjacent. Those. the quadrilateral ABDC cannot be denoted (B and D are not adjacent vertices).
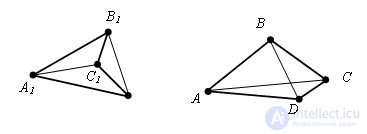
The quadrilaterals A1B1C1D1 and ABCD are distinguished by the fact that one diagonal intersects and the other does not. Quadrilaterals whose diagonals intersect will be called convex. The sum of the lengths of all sides of the quadrilateral will be called the perimeter. P = AB + BC + CD + DA.


Comments
To leave a comment
Planometry
Terms: Planometry