Theorem
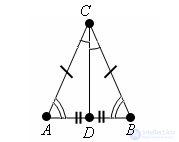
In an isosceles triangle, the median drawn to the base is a bisector and height.
 Evidence.
Evidence.
Let ABC be an isosceles triangle, and CD the median drawn to the base AB of that triangle.
Triangles ACD and BCD are equal by the first sign of equality of triangles, since AC = AB - because ABC is isosceles, AD = DB - because CD is the median and splits the base AB in half, ∠ CAD = ∠ CBD - because ABC is isosceles.
From the equality of triangles follows:
1) since ∠ ACD = ∠ BCD, then CD is a bisector;
2) since ∠ CDA = CDB and these angles are adjacent, they are 90 ° and CD is the height.
The theorem is proved.

Comments
To leave a comment
Planometry
Terms: Planometry