The main geometric figures on the plane are a
point and a
straight line .
Points are denoted by capital Latin letters: A, B, C, ....
Straight lines are denoted by lowercase Latin letters a, b, c, ....
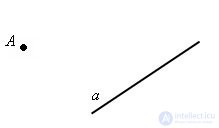
The line is infinite. The figure shows only its part, but we imagine it to be unlimitedly extended in both directions.
Axiom 1 Whatever the line, there are points belonging to this line and points that do not belong to it.
Axiom 2 You can draw a straight line through any two points, and only one.
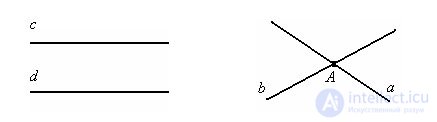
If two straight lines have a common point, then they say that they intersect.
If two straight lines do not have common points, then they say that they do not intersect.
Line a intersects line b at point A. A is the intersection point of lines a and b.
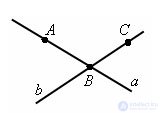
Points A and B belong to a. Longing C does not belong to a straight line a.
Accordingly, points C and B belong to line b. Longing A does not belong to b.
Points A and B also say lie on the line a, and point C does not lie.
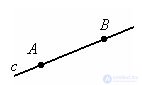
The straight line can be designated by two points lying on it. Direct with can be designated AB.




Comments
To leave a comment
Planometry
Terms: Planometry