Theorem Equal vectors have equal corresponding coordinates.
Evidence Consider two cases: 1) the vectors do not lie on one straight line.
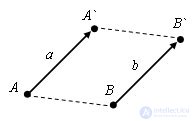
Let there be a vector a with origin at point A (x; y) and end at point A` (x`; y`). With parallel translation we get the vector b, which then has a beginning at the point B (x + c; y + d), and an end at the point B` (x` + c; y` + d). This shows that both vectors will have one and you coordinates (xx`; yy`).
2) the vectors lie on one straight line.
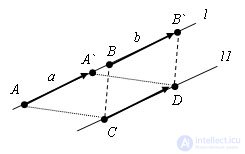
Let there be a line l on which equal vectors AA` and BB` lie. A (x; y), A` (x`; y`), B (x1; y1) and B (x1`; y1`). Let's draw the straight line l1 parallel to l and lay on it the vector CD equal to AA` and BB`, C (x0; y0) and D (x0`; y0`). Since AA `= CD, from the previous paragraph xx` = x0-x0` and yy` = y0-y0`. On the other hand, BB` = CD and x1-x1` = x0-x0`, y1-y1` = y0-y0`. Comparing equalities we get xx` = x1-x1` and yy` = y1-y1`. The theorem is proved.


Comments
To leave a comment
Planometry
Terms: Planometry