The outer corners of the triangle

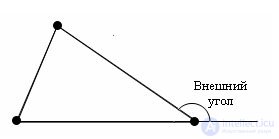
The external angle of the triangle at a given vertex is the angle adjacent to the angle of the triangle at this vertex.

Theorem

The external angle of the triangle is equal to the sum of the two angles of the triangle not adjacent to it.



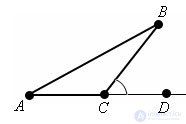Evidence. Let ABC be a given triangle. By the theorem on the sum of angles in a triangle
∠ ABС + ∠ BCA + ∠ CAB = 180 º.
this implies
∠ ABС + ∠ CAB = 180 º - ∠ BCA = BCD
The theorem is proved.

From the theorem it follows:
The external angle of the triangle is greater than any angle of the triangle that is not adjacent to it.