A segment is a part of a line that consists of all points of this line lying between its two given points, which are called the ends of the segment.
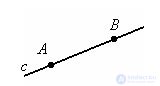
Points of line a located between points A and B are called the “segment AB”. A and B are the ends of the segment AB.
Axiom 3 Of the three points on the line, one and only one lies between the other two.
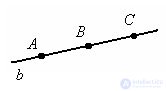
There are three points A, B and C on the line b. Point B lies between points A and C, or we can say that point B separates points A and C. In other words, A and C lie on opposite sides of point B.
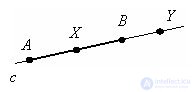
On a line with a point X lies between points A and B, you can say X belongs to the segment AB. The point Y does not lie between points A and B, so it does not belong to the segment AB.
Axiom 4 Each segment has a specific length greater than zero. The length of a segment is equal to the sum of the lengths of the parts into which it is divided by any of its points.
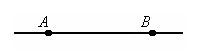
The distance between two points A and B is the length of the segment AB.
Moreover, if points A and B coincide, we will assume that the distance between them is zero.
Two segments are called equal if their lengths are equal.
If we take a point on the segment AB, let it be point C. Then the length of the segment AB is equal to the sum of the lengths of the segments AC and CB. This can be written as AB = AC + CB
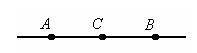
Usually the word segment is not written, but the names of the ends of the segments are written in square brackets. Those. You can write the "segment AB" or [AB].





Comments
To leave a comment
Planometry
Terms: Planometry