Angle is a figure that consists of a point (vertex of an angle) and two rays (sides of an angle) emanating from this point.
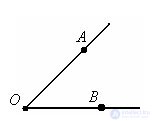
The angle is indicated by three points “AOB angle”: one any point on one of the rays of the angle (point A), the vertex of the angle (point O) and one point on the other ray of the angle (point B) are taken. You can designate this angle as the “BOA angle”. The entry “AOB angle” and “BOA angle” denote the same angle. In place of the word angle use the sign ∠. AOB angle can be written as:
1. ∠АОВ, ∠ВОА;
2. ∠O - point O is the vertex of the angle;
3. ∠ (ab) - a and b rays of an angle.
Angle breaks the plane into two parts. Each part is called a flat angle. Additional angles are called flat angles with common sides.
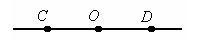
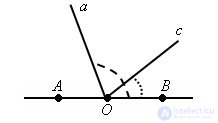
If the sides of the corner are additional half-lines in one straight line, then the angle is called unfolded. The angle of the CD is the unfolded angle with the vertex O.
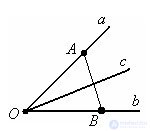
A ray is said to pass between the sides of a given angle, if it comes from its top and intersects some segment with ends on the sides of the angle. The beam c originates from point O, passes between the sides of the angle ab and intersects the segment AB.
Axiom
Each angle has a certain degree measure, greater than zero. The developed angle is 180 °. The degree measure of the angle is equal to the sum of the degree measures of the angles into which it is broken by any ray passing between its sides.
Angles are measured in degrees.
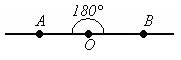
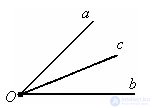
The angle (ab) is equal to the sum of the angles (ac) and (cb). ∠ (ab) = ∠ (ac) + ∠ (cb).
Axiom
From any beam into a given half-plane, you can postpone an angle with a given degree measure, less than 180 °, and only one.






Comments
To leave a comment
Planometry
Terms: Planometry