Theorem The angle inscribed in a circle is equal to half the corresponding central angle.
 Evidence.
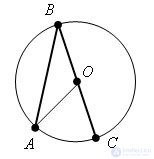
Evidence. Let there be a circle centered at the point O and an angle ABC inscribed in this circle, so that one of the sides of the angle passes through the center of the circle.
Connect point A with the center of the circle with point O. Δ ABO is isosceles (BO = AO as radii). Therefore, ∠OBA = ∠OAB. The external angle at the vertex O, the angle AOC is equal to the sum of the angles OBA and OAB. Means
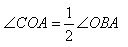
In general, there may be two options where the sides of the corner do not pass through the center of the circle. We will hold the auxiliary diameter BD
Option 1:
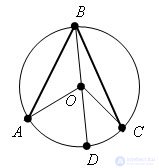
Then
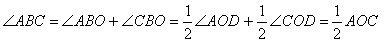
Option 2:
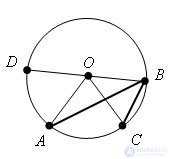
Then
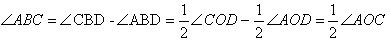
The theorem is proved.

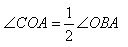

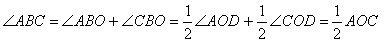

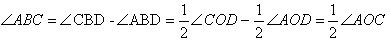
Comments
To leave a comment
Planometry
Terms: Planometry