Lecture
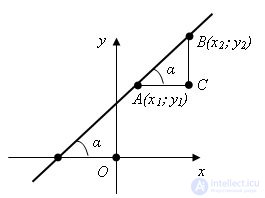
The angular coefficient in an equation of a straight line (also known as the slope or gradient) has a geometric meaning related to the inclination or steepness of the line. In simple terms, it determines how the line tilts or slants with respect to the horizontal axis on a graph.
The geometric meaning of the angular coefficient can be described as follows:
Positive Value: If the angular coefficient is positive, it means the line is slanting upward from left to right. In other words, as you move from left to right along the line, the y-values increase.
Negative Value: If the angular coefficient is negative, it means the line is slanting downward from left to right. In this case, as you move from left to right along the line, the y-values decrease.
Zero Value: When the angular coefficient is zero, the line is horizontal, and it does not tilt in either direction. The line is parallel to the x-axis.
Undefined or Infinite Value: If the angular coefficient is undefined or infinite, the line is vertical, and it does not tilt horizontally. The line is parallel to the y-axis.
So, the angular coefficient essentially quantifies the rate at which the y-coordinate changes concerning the x-coordinate as you move along the line. It provides information about the steepness and direction of the line in the Cartesian plane.
We transform the equation of the straight line ax + by + c = 0 to the form
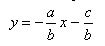
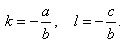
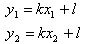
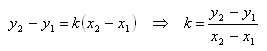
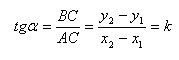
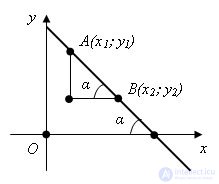
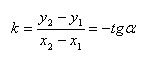
Comments
To leave a comment
Planometry
Terms: Planometry