 Theorem
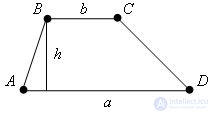
Theorem The area of the trapezoid is equal to the half-sum of its bases and the height
 Evidence
Evidence 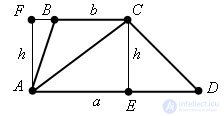
Let ABCD be a trapezoid.
The diagonal of the AC trapezoid divides it into two triangles: ABC and CDA. Consequently, the area of a trapezoid is equal to the sum of the areas of these triangles.
The area of the ACD triangle is
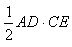
The area of the triangle ABC is equal to
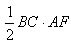
The heights AF and CE of these triangles are equal to the distance h between the parallel lines BC and AD, i.e. height of the trapezoid. Consequently,
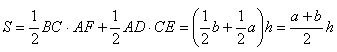
The theorem is proved.

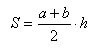

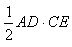
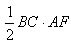
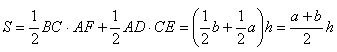
Comments
To leave a comment
Planometry
Terms: Planometry