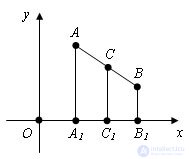
Let A (x1; y1) and B (x2; y2) be two arbitrary points, and C (x; y) be the midpoint of the segment AB. Draw through points A, B and C straight parallel to the y axis. They persect the x-axis at points A1, B1 and C1. According to the Thales theorem, the point C1 will be the middle of the segment A1B1. C1A1 = C1B1 and therefore | x-x1 | = | x-x2 |. It follows that either x-x1 = x-x2, or x-x1 = - (x-x2). The first equality is impossible, since x1 ≠ x2. Therefore, the latter is true and therefore
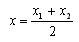
We also get that
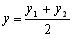

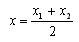
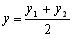
Comments
To leave a comment
Planometry
Terms: Planometry