Ball symmetry

Theorem

Any diametrical plane of the ball is its plane. The center of the ball is its center of symmetry.



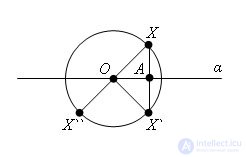
Evidence

Let α be the diametrical plane and X be an arbitrary point of the ball. We construct the point X` symmetric to the point X with respect to the segment XX` and intersects with it in its middle. From the equality of right triangles OAX and OAX`, it follows that OX` = OX.
Since OX ≤ R, then OX` ≤ R, i.e. the point symmetric to the point X belongs to the ball. The first assertion of the theorem is proved.
Now let X`` be a point symmetric to X with respect to the center of the ball. Then OX`` = OX ≤ R, i.e. point X`` belongs to the ball. The theorem is proven completely.

See also

• Ball
• Central symmetry of the parallelepiped
• The symmetry property about a point
• Symmetry relatively straight
• Symmetry about point