Theorem 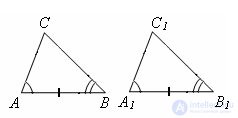
If the side and the corners of one triangle adjacent to it are equal, respectively, to the side and the corners of the other triangle adjacent to it, then such triangles are equal.
Evidence. Let triangles ABC and A1B1C1 ∠ A = ∠ A1, B = B1, AB = A1B1.
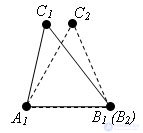
Let A1B2C2 be a triangle equal to a triangle ABC. The vertex B2 is located on the ray A1B1, and the vertex C2 is in the same half-plane with respect to the straight line A1B1, where the vertex C1 lies. Since A1B2 = A1B1, the vertex B2 coincides with the vertex B1. Since ∠ B1A1C2 = ∠ B1A1C1 and ∠ A1B1C2 = ∠ A1B1C1, the beam A1C2 coincides with the beam A1C1, and the beam B1C2 coincides with the beam B1C1. It follows that the vertex C2 coincides with the vertex C1. Triangle A1B1C1 coincides with triangle A1B2C2, and therefore is equal to triangle ABC. The theorem is proved.


Comments
To leave a comment
Planometry
Terms: Planometry