Addition of vectors. Parallelogram rule

The following method is called the parallelogram rule of vector addition:
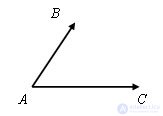
Let there be vectors AB and AC for which the beginning of the vector coincides, and the ends do not coincide.



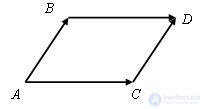
We complete this angle to a parallelogram, so AC = BD and AB = CD.



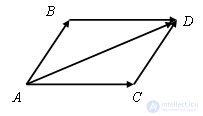
Then AB + BD = AD, and since BD = AC, then AB + AC = AD