Rhombus. Signs of rhombus.

A rhombus is a parallelogram, in which all sides are equal.



Theorem.

If the diagonal of a parallelogram is perpendicular, then the parallelogram is a rhombus.



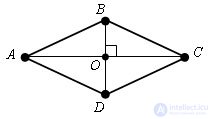
Evidence.

Let ABCD be a given parallelogram and AC ⊥ BD.
Δ AOB = Δ COB by the first sign of equality of triangles (∠ AOB = BOC, by condition, AO = OC - by the property of the parallelogram diagonals, BO is common). Therefore, AB = BC. By the property of the opposite sides of the parallelogram AB = DC, BC = AD, i.e. all sides are equal, it means ABCD - rhombus. The theorem is proved.

Theorem.

If the diagonal of a parallelogram is the bisector of its angle, then the parallelogram is a rhombus.



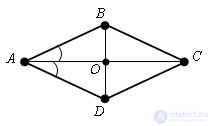
Let ABCD be a given parallelogram and ∠ CAB = ∠ CAD.
∠ CAD = ∠ ACB as internal crosswise under direct lines BC and AD and secant AC. By the condition ∠ CAB = ∠ CAD, it follows that Δ ABC is isosceles (∠ CAB = ∠ ACB, a sign of an isosceles triangle). Therefore, AB = BC. Since ABCD is a parallelogram, AB = CD, BC = AD. Then AB = BC = CD = AD. Thus, ABCD is a rhombus. The theorem is proved.