Theorem. Whatever the three points, the distance between any two of these points is not more than the sum of the distances from them to the third point.
Evidence. Let A, B and C be the given three points.
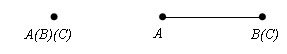
If two currents out of three or all three points coincide, then the statement of the theorem is obvious.

If all points are different and lie on one straight line, then AB + BC = AC. This shows that each of the three distances is not greater than the sum of the other two.
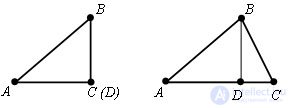
If three points do not lie on one straight line, we prove that AC
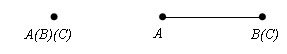


Comments
To leave a comment
Planometry
Terms: Planometry