The third sign of equality of triangles

Theorem

If the three sides of one triangle are equal respectively to the three sides of another triangle, then such triangles are equal.



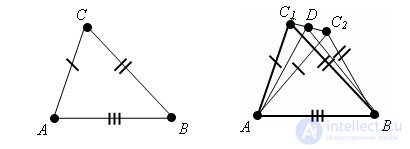
Evidence.

Let triangles ABC and A1B1C1 be such that AB = A1B1, AC = A1C1, BC = B1C1. It is required to prove that the triangles are equal.
Suppose that the triangles are not equal. Then ∠ A ≠ ∠ A1, ∠ B ≠ ∠ B1, ∠ C ≠ ∠ C1 simultaneously. Otherwise, the triangles would be equal in the first sign.
Let the triangle A1B1C2 be a triangle equal to the triangle ABC whose vertex C2 lies in the same half-plane with vertex C1 relative to the straight line A1B1.
Let D be the midpoint of the segment C1C2. triangles A1C1C2 and B1C1C2 are isosceles with common base C1C2. Therefore, their medians A1D and B1D are the heights. Hence, the straight lines A1D and B1D are perpendicular to the straight line C1C2. Straight lines A1D and B1D do not coincide, since points A1, B1, D do not lie on one straight line. But through point D of straight line C1C2 it is possible to draw only one straight line perpendicular to it. We have come to a contradiction. The theorem is proved.