Theorem The square of any side of the triangle is equal to the sum of the squares of the other two sides without doubling the product of these sides by the cosine of the angle between them.
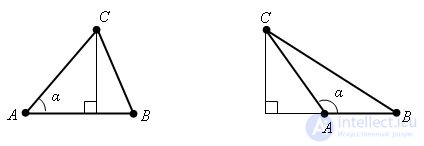 Evidence.
Evidence. Let there be Δ ABC.
Prove that
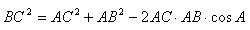
We have vector equality
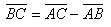
Square the left and right sides of the equation, we get
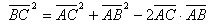
Or
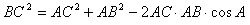
The theorem is proved.

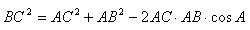
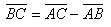
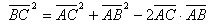
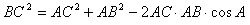
Comments
To leave a comment
Planometry
Terms: Planometry