The property of multiplying a vector by a number

Theorem

The absolute value of the vector λa is equal to | λ | | a |. The direction of the vector λa for a ≠ 0 coincides with the direction of the vector a if λ> 0, and is opposite to the direction of the vector a if λ <0.



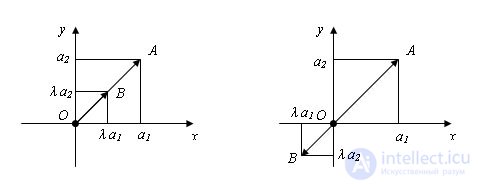
Evidence.

We construct the vectors OA and OB equal to a and λa, respectively (O is the origin). Let a1 and a2 be the coordinates of a. Then the coordinates of the point A are the numbers a1 and a2; the coordinates of the point B are the numbers λa1 and λa2. The equation of the line OA has the form: αx + βy = 0.
Since the coordinates of the point A (a1; a2) satisfy the equation, the coordinates of the point B (λa1; λa2) also satisfy it. It follows that point B lies on the line OA. The coordinates c1 and c2 of any point C lying on the ray OA have the same signs as the coordinates a1 and a2 of point A, and the coordinates of any point that lies on the ray complementary to OA have opposite signs.
Therefore, if λ> 0, then the point B lies on the ray OA, and therefore, the vectors a and λa are equally directed. If λ <0, then point B lies on the additional ray and vectors a and λa are oppositely directed.
The absolute value of the vector λa is equal to:



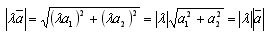
The theorem is proved.