Theorem If two angles of one triangle are equal to two angles of another triangle, then such triangles are similar.
 Evidence.
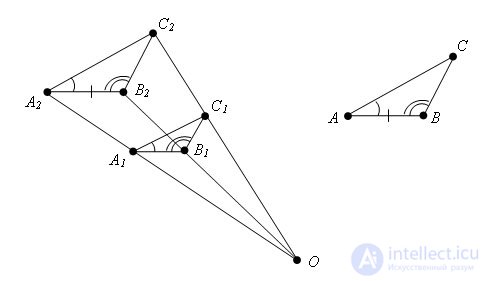
Evidence. Let the triangles ABC and A1B1C1 CAB = ∠ C1A1B1, ABC = ∠ A1B1C1. Let us prove that Δ ABC is similar to Δ A1B1C1.
Let k = AB / A1B1. Subject Δ A1B1C1 homothety with coefficient k. Get some Δ A2B2C2.
Δ A2B2C2 = Δ ABC by the second sign of equality of triangles (∠ C2A2B2 = ∠ C1A1B1 = ∠ CAB, ∠ A2B2C2 = ∠ A1B1C1 = ∠ ABC because the similarity transformation preserves angles, A2B2 = k * A1B1 = AB, by condition).
Triangles A1B1C1 and A2B2C2 are homothetic, hence similar. Δ A2B2C2 = Δ ABC, therefore are similar too, which means that triangles A1B1C1 and ABC are similar. The theorem is proved.

Comments
To leave a comment
Planometry
Terms: Planometry