Motion properties

Theorem.

Points that lie on a line, when moving, move to points that lie on a line, and the order of their relative position is preserved.

Evidence.

Let there be three points A, B and C, which lie on one straight line and point B lies between points A and C.
We prove that the points A`, B` and C` lie on one straight line.
If the points A`, B` and C` do not lie on one straight line, then these points are the vertices of the triangle. Therefore, A`C` <a`b` + b`c`. By = "" definition = "" movement = "" follows, = "" that = "" ac <ab + bc, = "" but = "" by = "" property = "" dimension = "" segments = "" ac = "AB + BC," contradicts = "" our = "" assumption, = "" therefore = "" point = "" b` = "" lies = "" on = "" straight line = "" a`c` . = "" <br = ""> Prove that B` lies between A `and C`. Then the equalities AB = A`B`, AC = A`C`, BC = B`C`, AB + BC = AC are true. It follows that A`B` + B`C` = A`C`. This means that point B` lies between points A `and C`. The theorem is proved.

Corollary of the theorem

1. The line segment is translated into a segment.
2. When moving, the beam goes into the beam, the straight line goes into the straight line.
3. The triangle is translated by movement into a triangle.

Theorem.

When moving, the angles between the half-lines are preserved.



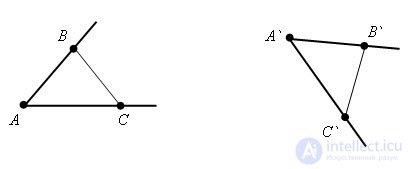
Suppose that the half-lines AB and BC do not lie on one straight line and form an angle. When moving, the half-lines turn into A`B` and A`C` respectively. Conduct a segment of BC and B`C`. We obtain the triangle ABC and A`B`C`. Since the distances are saved during the movement, the triangles ABC and A`B`C` are equal by the third sign of equality of triangles, and therefore the angles ABC and A`B`C` are equal. The theorem is proved