Thales theorem

Theorem.

If parallel straight lines intersecting the sides of an angle cut equal segments on one side of them, then they cut off equal segments on the other side of it.



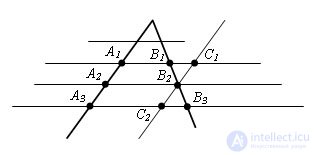
Evidence.

Let points A1, A2, A3 be the intersection points of parallel lines on one side of an angle. And the points B1, B2, B3 are the corresponding points of intersection of these straight lines with the other side of the angle. We prove that if A1A2 = A2A3, then B1B2 = B2B3.
Let us draw a straight line C1C2 through point B2 parallel to the straight line A1A2. We obtain parallelograms A1C1BA2 and A2B2C2A3. According to the properties of the parallelogram, A1A2 = C1B2 and A2A3 = B2C2. Since A1A2 = A2A3, then C1B2 = B2C2.
Δ C1B2B1 = Δ C2B2B3 basis of equality of the second triangles (C1B2 = B2C2, ∠ C1B2B1 = ∠ C2B2B3, as vertical, ∠ B1C1B2 = ∠ = B3C2B2, as inner lying crosswise in direct B1C1 and C2B3 and secant S1S2). From the equality of triangles it follows that B1B2 = B2B3. The theorem is proved.