The straight line passing through the midpoint of a segment perpendicular to it is called the median perpendicular or mediatrix .
Theorem.
The middle perpendiculars to the two sides of the triangle intersect.
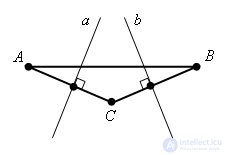
Evidence.
Suppose there are Δ ABC and the lines a, b are the perpendicular bisectors of the sides of this triangle.
Assume that the lines a and b do not intersect, which means a || b. AC ⊥ a, BC ⊥ b, which means BC ⊥ a, since a || b. Thus, both straight lines AC and BC ⊥ a, and so are parallel. And this is not true, since AC and BC intersect at point C. We have come to a contradiction. The theorem is proved. |
|
Comments
To leave a comment
Planometry
Terms: Planometry