Theorem
The area of a circle is equal to half the product of the length of the circumscribing circle by the radius.
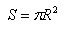 Evidence
Evidence
We construct two regular n-gons: P1 is inscribed in a circle and P2 is described near a circle.
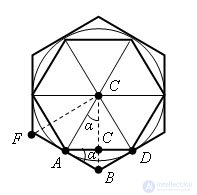
Polygons P1 and P2 are simple shapes. Polygon P2 contains a circle, and polygon P1 is contained in a circle. The radii drawn at the vertices of the polygon divide it into n triangles equal to the triangle AOD. therefore
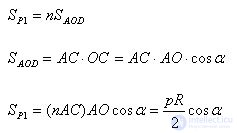
where p is the perimeter of the polygon P1, R is the radius of the triangle. Similarly, we find the area of the polygon P2
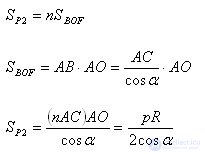
So, the polygon P1 contained in a circle has an area
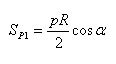
And the polygon P2 containing the circle has area
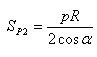
If n is sufficiently large, the perimeter p differs arbitrarily small from the circumference l of the circle, and cos α differs from the unit arbitrarily little, therefore the areas of the polygons P1 and P2 differ slightly from the value of lR / 2. According to the definition of the area of an arbitrary figure, this means that the area of a circle
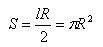
The theorem is proved.
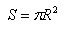

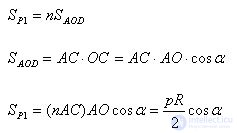
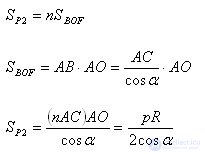
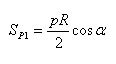
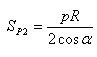
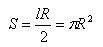
Comments
To leave a comment
Planometry
Terms: Planometry