Parallelogram. Signs of parallelogram

A parallelogram is a quadrilateral whose opposite sides are parallel in pairs.



Theorem.

If the diagonals of the quadrilateral intersect and the intersection point is divided in half, then this quadrilateral is a parallelogram.



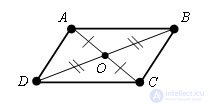Evidence.

Let ABCD be the given parallelogram, O be the intersection point of the diagonals of the given parallelogram.
Δ AOD = Δ COB by the first sign of equality of triangles (OD = OB, AO = OC by the condition of the theorem, ∠ AOD = COB, as vertical angles). Therefore, ∠ OBC = ∠ ODA. And they are internal crosswise lying for direct AD and BC and secant BD. On the basis of parallelism, straight lines AD and BC are parallel. We also prove that AB and DC are also parallel. By definition, this quadrilateral parallelogram. The theorem is proved.

Theorem.

If a quadrilateral pair of opposite sides are parallel and equal, then the quadrilateral is a parallelogram.



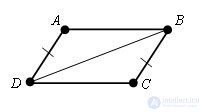
Let ABCD be a given quadrilateral. AD parallel to BC and AD = BC.
Then Δ ADB = Δ CBD on the first sign of equality of triangles (ADB = CBD, as internal crosswise lying between the straight lines AD and BC and the secant DB, AD = BC by condition, DB - common).
Therefore, ∠ ABD = ∠ CDB, and these angles are internal crosswise lying for straight lines AB and CD and secant DB. By the theorem, the parallel property of lines AB and CD are parallel. So ABCD is a parallelogram. The theorem is proved.

Theorem.

If the opposite angles are equal in a quadrilateral, such a quadrilateral is a parallelogram.



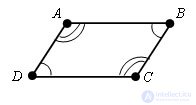Evidence.

Let quadrilateral ABCD be given. ∠ DAB = ∠ BCD and ∠ ABC = CDA.



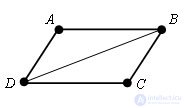
Let's draw a diagonal DB. The sum of the angles of the four square is equal to the sum of the angles of the triangles ABD and BCD. Since the sum of the angles in the triangle is 180 º,
∠ DAB + ∠ BCD + ∠ ABC + ∠ CDA. = 360 º. Since the opposite angles in the quadrilateral are equal, then ∠ DAB + # 8736 ABC = 180 º and ∠ BCD + ∠ CDA = 180 º.
The angles BCD and CDA are internal one-sided for the straight lines AD and BC and the secant DC, their sum is 180 º, therefore from the corollary to the theorem on the parallelism of straight lines, the straight lines AD and BC are parallel. It is also proved that AB || DC. Thus, the quadrilateral ABCD is a parallelogram by definition. The theorem is proved.