With an unlimited increase in the sides of a regular polygon, its perimeter approaches the perimeter of the circle.
 Theorem
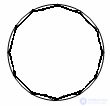
Theorem The ratio of the circumference of a circle to its radius does not depend on the circle.
Evidence. Take two arbitrary circles with radii R1 and R2 and lengths l1 and l2. Let's pretend that
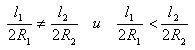
We write in the circle the correct n-gons. N is so large that the perimeters p1 and p2 of regular polygons approach the lengths of circles l1 and l2. Therefore, we replace the circumference lengths by the perimeters, then
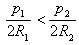
But the perimeters of regular convex n-gons are referred to as the radii of the circumscribed circles:
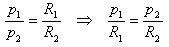
That contradicts the assumption. The theorem is proved.
The ratio of the circumference to diameter is denoted by the Greek letter π.
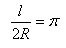

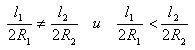
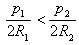
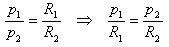
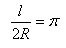
Comments
To leave a comment
Planometry
Terms: Planometry