Properties of parallel lines

Theorem

Two straight lines, parallel to the third, are parallel.



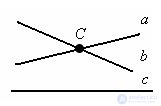Evidence.

Let lines a and b be parallel to line c. Assume that the lines a and b are not parallel. Then they intersect at some point C. It turns out that through point C there pass two straight lines parallel to c. But this contradicts the axiom "Through a point that is not lying on a given line, you can draw on a plane no more than one line parallel to this one." The theorem is proved.

Theorem

If two parallel straight lines are crossed by the third straight line, then the inner crosswise lying angles are equal.



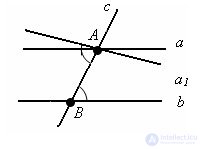Evidence.

Let there be parallel lines a and b that intersect the secant line c. The line c intersects the line a at the point A and the line b at the point B. Draw the line a1 through the point A so that the lines a1 and b with the secant c form equal inner crosswise lying angles. On the basis of parallelism, straight lines a1 and b are parallel. And since through point A it is possible to draw only one straight parallel b, a and a1 coincide.
Hence, the internal crosswise lying angles formed by a and b are equal. The theorem is proved.

Based on the theorem, it is proved:

If two parallel lines are crossed by the third line, then the corresponding angles are equal.

If two parallel straight lines are crossed by the third straight line, then the sum of the inner one-sided angles is 180 º