Parallelogram area

Theorem

The area of ​​the parallelogram is equal to the product of its side by the height drawn to this side S = a • h.

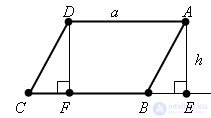
Evidence

Let ABCD be a given parallelogram. If it is not a rectangle, then one of its angles A or B is sharp. For definiteness, let A be sharp.
We drop the perpendicular AE from the vertex A to the straight line CB. The area of ​​the trapezoid AECD is equal to the sum of the areas of the parallelogram ABCD and the triangle AEB. Drop the perpendicular DF ​​from the vertex D to the straight CD. Then the area of ​​the trapezoid AECD is equal to the sum of the areas of the rectangle AEFD and the triangle DFC. Right triangles AEB and DFC are equal, which means they have equal areas. It follows that the area of ​​the parallelogram ABCD is equal to the area of ​​the rectangle AEFD, i.e. equal to AE • AD. The segment AE is the height of the parallelogram corresponding to the side AD, and, therefore, S = a • h. The theorem is proved.