The existence and uniqueness of the perpendicular to the line

Theorem.

From any point not lying on this straight line, you can drop perpendicular to this straight line, and only one.

Evidence



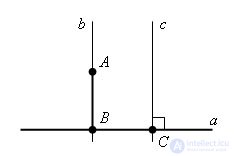
Let a be a given straight line and a point A. which is not lying on this straight line. Let us draw a straight line c through it to some point of a straight line perpendicular to it. The line c intersects the line a at point C. Now we draw the line parallel to line b, so that line b passes through point A. Then line b ⊥ a, since b || with and with ⊥ a.
Hence the segment AB ⊥ a.
Now we prove the uniqueness of the perpendicular AB.



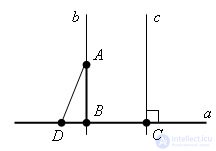
Suppose there is also a perpendicular passing through point A to the line a.
Then the triangle ABD will have two angles of 90 °. And this can not be, since the sum of all angles in a triangle is 180 °. The theorem is proved