Circle properties

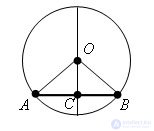
Theorem.

The diameter of the circle passing through the middle of the chord, which is not a diameter, is perpendicular to it.



Evidence.

Let AB be the chord of a circle and C its midpoint. The triangle AOB is isosceles with base AB, since AO = OB as radii. By the property of the median of an isosceles triangle drawn to the base, the segment OC is the height. Therefore, the diameter of a circle drawn through the middle of the chord is perpendicular to the chord. The theorem is proved.

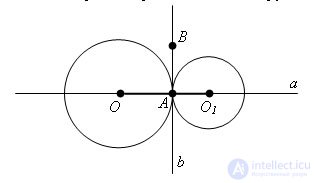
Theorem.

The straight line drawn through the centers of the circumscribing circles passes through the point of their touch.



Evidence.

Connect the centers of the circles with their point of contact. We obtain two segments OA and O1A. A common tangent b to these circles passes through point A of tangency of two circles. Let B be a point on a line b. Then ∠ BAO1 = ∠ BAO = 90 °. Therefore, the angle of OAO1 is expanded and the points O, A, O1 lie on one straight line a, perpendicular to the tangent b. The theorem is proved.