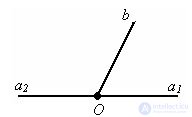
Two corners are called adjacent if they have one side in common, and the other sides are additional rays. In the figure (a2b) and (a1b) adjacent angles.
Theorem The sum of adjacent angles is 180 ?.
Evidence.
Let ∠ (a2b) and ∠ (a1b) be adjacent angles. Semidirect b splits the unfolded angle (a1a2) into two angles. This means that ∠ (a2b) + ∠ (a1b) = (a1a2) = 180 ?. Those. the sum of adjacent angles is 180 ?. The theorem is proved.
 Theorem
Theorem
If the two angles are equal, then the angles adjacent to it are equal.
Evidence.
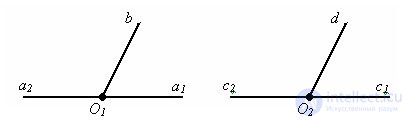
Angles ∠ (a2b) and ∠ (a1b) are adjacent angles and ∠ (c2d) and ∠ (c1d) are also adjacent angles.
Let ∠ (a1b) = (c1d). But it follows from the previously proved that ∠ (a1b) + ∠ (a2b) = 180 ° and ∠ (c1d) + ∠ (c2d) = 180 °. Then ∠ (a1b) = 180 ° - ∠ (a2b) and ∠ (c1d) = 180 ° - ∠ (c2d). And the angles ∠ (a1b) and ∠ (с1d) are equal, hence 180 ° - ∠ (a2b) = 180 ° - ∠ (с2d). This shows that ∠ (a2b) = ∠ (c2d). The theorem is proved.
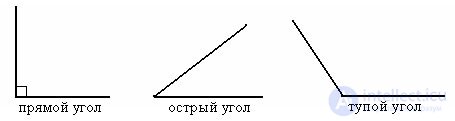
An angle is called acute if its degree measure is greater than 0 ° but less than 90 °.
An angle is called obtuse if its degree measure is more than 90 ° but less than 180 °.
An angle of 90 ° is called a right angle.
If the angle is acute, then the angle adjacent to it is obtuse and vice versa.
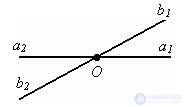
Two angles are called vertical if the sides of one angle are additional half-lines of the other angle. The pairs of angles ∠ (a2b2) and ∠ (a1b1), ∠ (a2b1) and ∠ (a1b2) are vertical angles.
Theorem.
Vertical angles are equal.
Evidence.
Let ∠ (a2b2) and ∠ (a1b1) be vertical angles. The angle (a2b1) is adjacent ∠ (a2b2) and ∠ (a1b1) and complements them to 180 °, according to the theorem on the sum of adjacent angles, therefore ∠ (a2b2) and ∠ (a1b1) are equal. The theorem is proved.
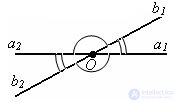
∠ (a2b2) = (a1b1), ∠ (a2b1) = (a1b2).
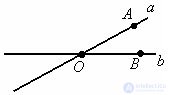
The angle between the lines a and b is the smaller of the angles with the vertex at the point O.
The angle between the straight lines a and b is the angle AOB.
 Two corners are called adjacent if they have one side in common, and the other sides are additional rays. In the figure (a2b) and (a1b) adjacent angles.
Two corners are called adjacent if they have one side in common, and the other sides are additional rays. In the figure (a2b) and (a1b) adjacent angles.




Comments
To leave a comment
Planometry
Terms: Planometry