Theorem. The middle line of the trapezoid is parallel to the bases and is equal to their half-sum.

Let ABCD be the given trapezoid. EF is the middle line of the trapezoid.
Draw through vertex B and point F a straight line. Let this straight line intersect the straight line AD at some point G.
Δ CFB = Δ FDG by the second criterion of equality of triangles (CF = FD, by construction, ∠ BCF = ВА PVA, as internal crosswise lying with parallel straight sun and DG and sectioning CD, ∠ CFB = ∠ DFG, as vertical). So BC = DG and BF = FG.
Therefore, the middle line of the trapezoid EF is the middle line of the triangle ABG. By the property of the center line of the triangle EF || AD, and
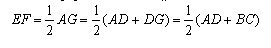
The theorem is proved.

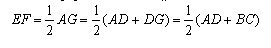
Comments
To leave a comment
Planometry
Terms: Planometry