The length of a perpendicular dropped from a given point to a straight line is called the distance from the daughter to the straight line.
Theorem. The distance from any two points of a straight line to a parallel straight line is equal.
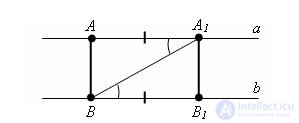
Let a and b be parallel lines and points A and A1 be some points on a line a. Let us drop perpendicular AB from point A onto line b and set segment BB1 from point B equal to AA1 so that A and B1 are on opposite sides of line A1B.
Δ A1AB = Δ BB1A1 on the first sign of the equality of triangles (A1B is common, ∠ AA1B = ∠ B1BA1 - as internal crosswise, AA1 = B1B).
It follows from the equality of triangles that A1B1 is also perpendicular to the straight line b and AB = A1B1. The theorem is proved.
The distance between parallel lines is the distance from any point of one straight line to another straight line.

Comments
To leave a comment
Planometry
Terms: Planometry